For the experts.

All the following equations and parameters are described in the Theory page.

Erosion and sedimentation in a river can be seen as resulting from the difference between the sediment load of a river, or in other words the flow of moving sediment (in m³/s or t/s for example) and a transport capacity of the river that would represent the maximum amount of sediment that the river can transport per unit of time (Bagnold, 1966). We can then determine a law for this transport capacity, and Bagnold (1966) and others have proposed from mechanistic considerations that this law depends on water flow and slope, among other things. We can then calculate this transport capacity on each cell of the model and calculate the difference between this capacity and the flux of sediment transported. If the difference is positive, this difference translates into erosion, if it is negative, into sedimentation. Several LEMs are parameterized in this way.

The approach in Cidre, as in other LEMs, is different but there is a link between the two formulations. In Cidre, it is not the transport capacity that is parameterized but the rates of detachment and deposition on a cell. In this view due to Einstein, H.A. (1937), water constantly exchanges sediment with the river bed, the flux of grains ”falling” depends on their settling rate into the water and the flux of grains ”rising” depends on the capacity of the water to detach grains from the rocky or alluvial river bed. But the notion of carrying capacity emerges from this view. Considering only the river processes without lateral erosion (cf Theory page.)

and because D_r =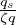

or

Where the transport capacity is defined (”emerges”) as

and because ϵ_r = Kq^mSⁿ

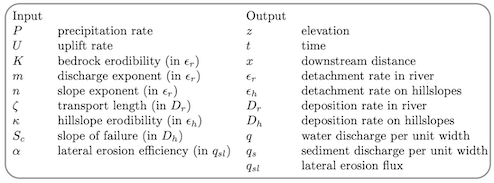
q_t depends on the water discharge and slope, as in the Bagnold’s model. Equation 4 shows that the transport capacity depends on the detachment rate and on the deposition length parameter ζ. The flux q_t is the maximum sediment flux that the river can carry. According to Equation 3 (known as the ”under-capacity model”), the erosion or sedimentation (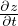) is not exactly the difference between the transport capacity (q_s) and the sediment flux (q_s). It is this difference divided by ζq. ζq is a transport or deposition length, difficult to define physically but which can be considered at first order as the length reached by a packet of sediment before settling for a long time. ζq can also be seen as the distance necessary for the flux of transported sediment to reach the maximum value, i.e. the transport capacity. Let’s imagine a situation where the river bed suddenly changes from a rocky to a sandy bed downstream. Sand will begin to be transported and the river clear water becomes cloudy. Then ζq represents the distance along the river for the sand transport to be optimal, i.e. the sediment flux is equal to the transport capacity, or in other words, the distance at which the water color is the darker and does not change downstream. The inertia of grain transport effectively imposes this distance. This ζq interpretation is conceptually different but mathematically strictly equivalent to the previous one. It can therefore be seen that the erosion-deposition model is richer and more realistic than the model not involving this transport length. Experts can read Charru et al. (2004); Davy and Lague (2009).

References